ReactorEnv

We define the reactor as a Continuous Stirred Tank Reactor (CSTR) Process Model, which provides the necessary conditions for a reaction to take place. Because it is a continuous process, reactants and products are continuously fed and withdrawn from the reactor respectively.

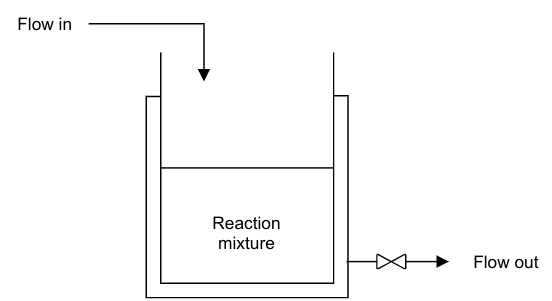
In this example, a single first order irreversible exothermic reaction of the form A → B takes place. Since the reaction is exothermic, thermal energy is removed from the reactor through a cooling jacket.

The following assumptions are taken in deriving the model:

• The reaction mixture is well mixed. This implies that there are no spatial variations in the reaction mixture.

• Negligible or no heat losses to the surroundings.

Performing a component balance on reactant A, the following ordinary differential equation is obtained

\[\frac{dc_A}{dt} =\frac{q_{in}}{\pi r^2h}(c_{Af} - c_A) - k_0 \exp(-\frac{E}{RT})c_A\]

where \(c_A\) is the concentration of reactant A in \(kmol/m^3\), \(t\) is the time in \(min\), \(q_{in}\) is the volumetric flow rate of the inlet stream in \(m^3/min\), \(r\) is the radius of the reactor in \(m\), \(h\) is the level of reaction mixture in the reactor in \(m\), \(c_{Af}\) is the concentration of reactant A in the feed stream in \(kmol/m^3\), \(k_0\) is the pre-exponential factor in \(min^{-1}\), \(E/R\) is the ratio of reaction activation energy to the universal gas constant in \(K\) and \(T\) is the reaction mixture temperature in \(K\).

Similarly, an energy balance can be conducted to obtain the following energy balance equation

\[\frac{dT}{dt} = \frac{q_{in}}{\pi r^2h}(T_{f} - T) + \frac{-\Delta H}{\rho c_p} k_0 \exp(-\frac{E}{RT})c_A + \frac{2U}{r\rho c_p}(T_c - T)\]

where \(T_f\) is the temperature of the feed stream in \(K\), \(\Delta H\) is the heat of reaction in \(kJ/kmol\), \(\rho\) is the density of the reaction mixture in \(kg/m^3\), \(c_p\) is the specific heat capacity of the reaction mixture in \(kJ/kg \cdot K\), \(U\) is the heat transfer coefficient in \(kJ/min \cdot m^2 \cdot K\) and \(T_c\) is the coolant temperature.

Finally, deriving an overall material balance around the reactor leads to the following equation

\[\frac{dh}{dt} = \frac{q_{in}-q_{out}}{\pi r^2}\]

where \(q_{out}\) is the volumetric flow rate of the contents out of the reactor in \(m^3/min\).

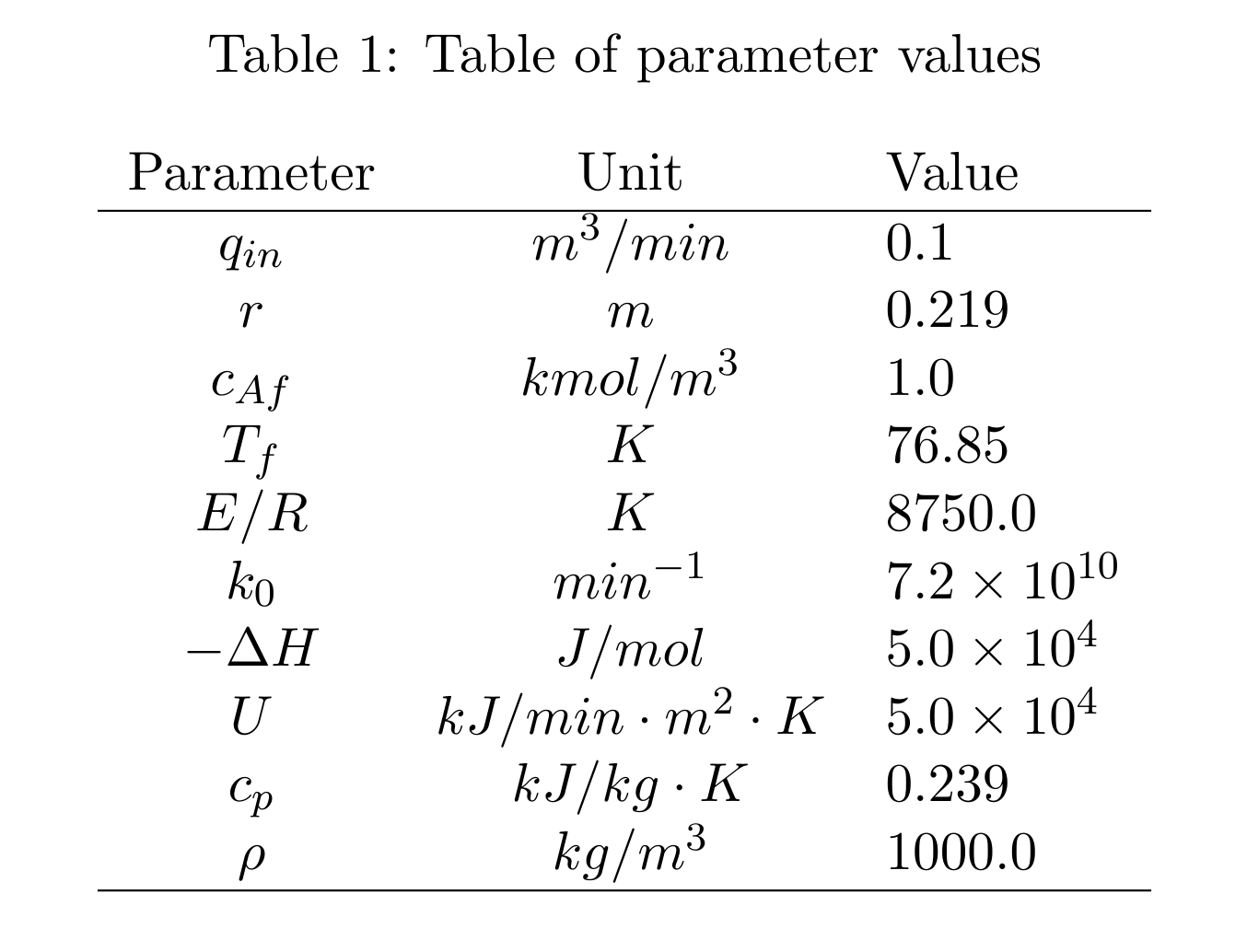
A summary of parameters values used in this project is presented in Table

In the CSTR process model described above, \(c_A\), \(T\), and \(h\) are the state variables. The controlled variables are \(c_A\) and \(h\) while the manipulated variables are \(q_{out}\) and \(T_c\).

ReactorEnv module

Following the above discription, we provide APIs as below: